
实际在 OpenGL 中的变换的一些记录,尤其是与 「GAMES101」Transformation 推导中的一些区别。其中旋转、平移等常见变换以及视图变换均是相同的。这里主要讨论正交投影和透视投影,以及法线变换矩阵的推导。
NDC 坐标 (Normalized Device Coordinates, 标准化设备坐标)
为了得到与 glm 中相同的结果,我们得先了解一下 NDC 坐标。在 OpenGL 中,标准化设备坐标是一个 $x, y, z$ 值在 $[-1, 1]$ 的一小段空间。需要注意的是,NDC 坐标是左手坐标系。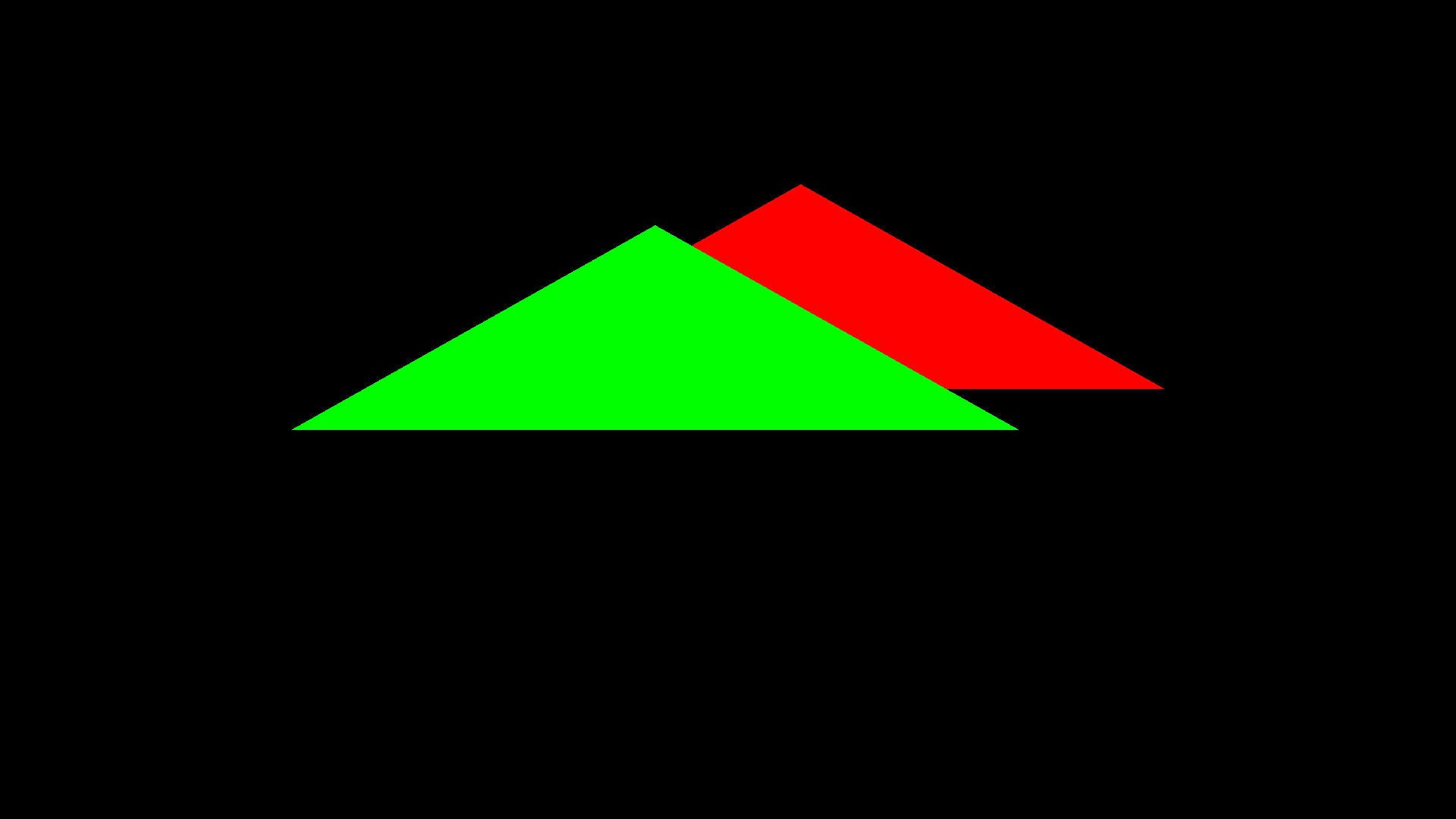
其中绿色三角形 $z$ 值为 $-0.5$,红色为 $0.5$,可以看出其为左手坐标系。
1 |
|
Orthographic projection (正交投影)
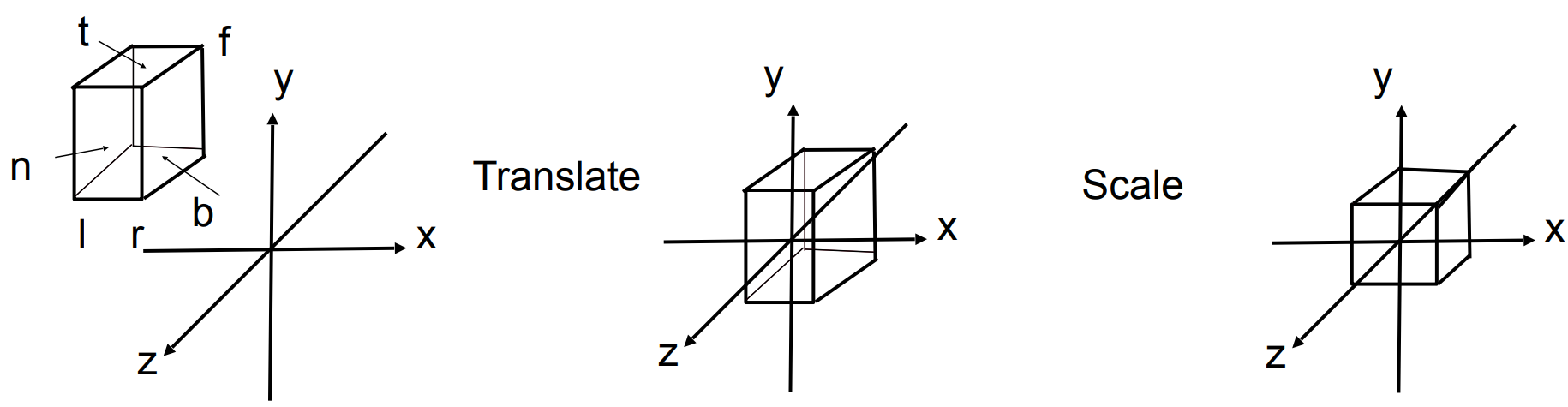
将 $[l, r] \times [b, t] \times \color{red}{[-n, -f]}$ (视野范围) 映射到 $[-1, 1] ^ 3$ 标准 (canonical) 立方体(映射到 NDC 坐标)。
注:与 GAMES101 推导不同,这里我们用 $-n, -f$ 表示近平面和远平面的 $z$ 值。
先平移,将中心移到原点,再缩放到 $[-1, 1] ^ 3$,缩放的同时将 $z$ 值取相反数以变换为 NDC 中的左手坐标系。
$$\begin{aligned} M_{ortho} &= \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & 0\\ 0 & \frac{2}{t - b} & 0 & 0\\ 0 & 0 & \color{red}{-\frac{2}{f - n}} & 0\\ 0 & 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & 0 & -\frac{r + l}{2}\\ 0 & 1 & 0 & -\frac{t + b}{2}\\ 0 & 0 & 1 & -\frac{n + f}{2}\\ 0 & 0 & 0 & 1 \end{bmatrix}\\ &= \begin{bmatrix} \frac{2}{r - l} & 0 & 0 & -\frac{r + l}{r - l}\\ 0 & \frac{2}{t - b} & 0 & -\frac{t + b}{t - b}\\ 0 & 0 & -\frac{2}{f - n} & -\frac{f + n}{f - n}\\ 0 & 0 & 0 & 1 \end{bmatrix} \end{aligned}$$与 glm 中一致
1 | template<typename T> |
Perspective projection (透视投影)
齐次坐标:$(x, y, z, 1), (kx, ky, kz, k \neq 0), (xz, yz, z ^ 2, z \neq 0)$ 都是同一个点
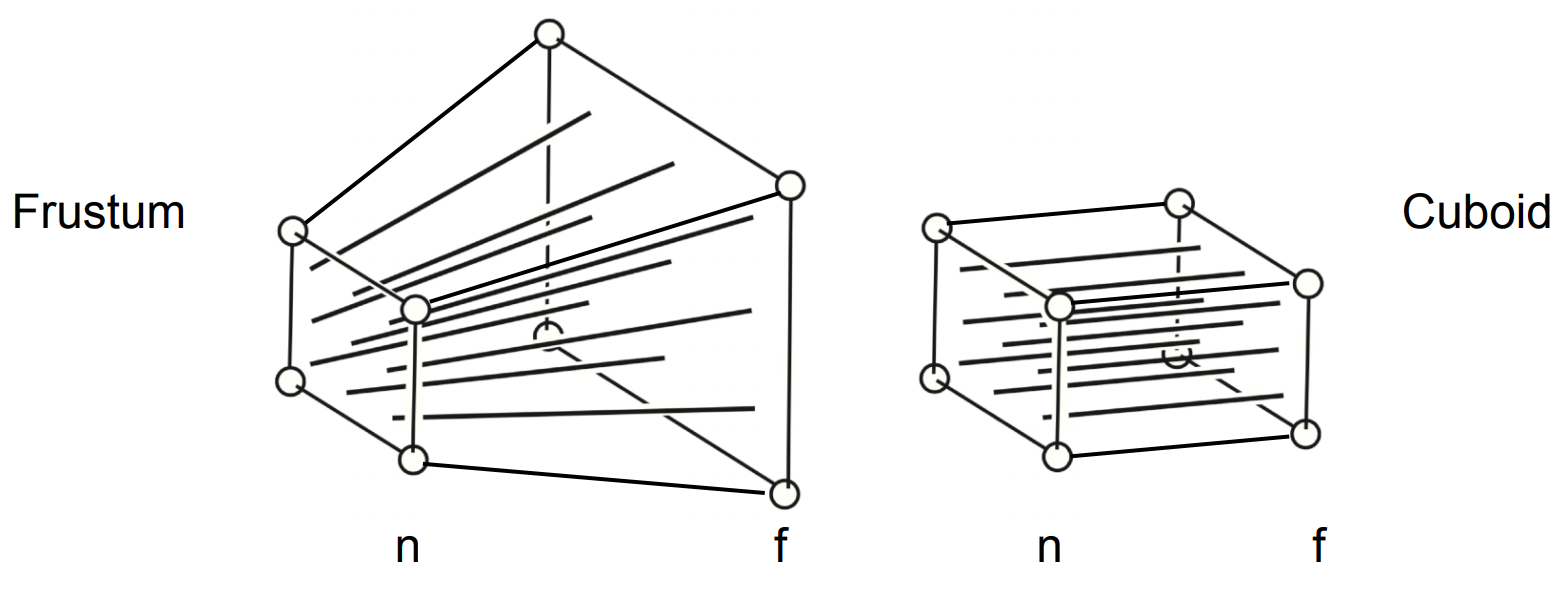
基本思路:将远平面挤压成和近平面同大小,再正交投影;近平面不会变,远平面中心点不会变
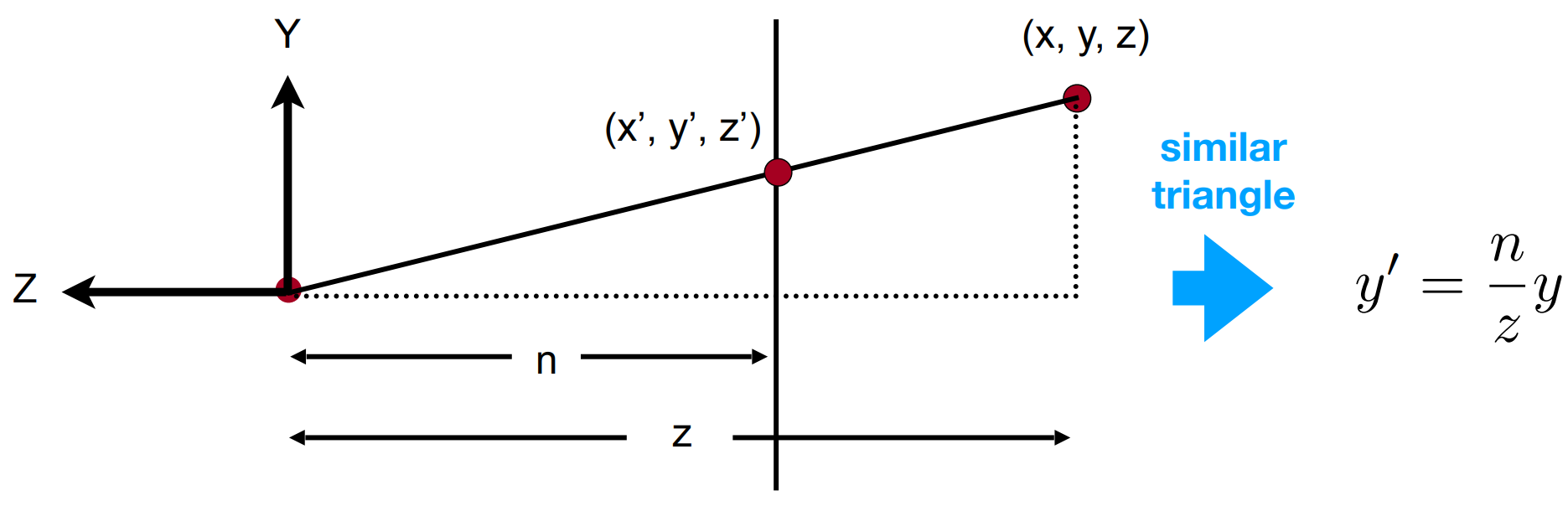
从侧面 ($x$) 看,上图右侧 $-z$ 方向即为相机看向的方向,由相似三角形可得
$$y’ = \color{red}{\left|\frac{n}{z}\right|}y$$
同理
$$x’ = \color{red}{\left|\frac{n}{z}\right|}x$$
所以
$$\begin{bmatrix} x\\y\\z\\1 \end{bmatrix} \Rightarrow \begin{bmatrix} \color{red}{-nx/z}\\\color{red}{-ny/z}\\\text{unknown}\\1 \end{bmatrix} = ^ {\times \color{red}{-z}}\begin{bmatrix} nx\\ny\\\text{still unknown}\\\color{red}{-z} \end{bmatrix}$$即求 $M_{persp \rightarrow ortho}$ 满足
$$M_{persp \rightarrow ortho} \begin{bmatrix} x\\y\\z\\1 \end{bmatrix}=\begin{bmatrix} nx\\ny\\\text{unknown}\\z \end{bmatrix}$$于是有
$$M_{persp \rightarrow ortho}=\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & \color{red}{-1} & 0 \end{bmatrix}$$注意到任何一个近平面上的点不变,任何一个远平面上的点 $z$ 不会发生变化
利用近平面不变
用 $n$ 替换上面坐标变换中的 $z$,即取进平面上点 $(x, y, -n, 1)$,有
对于 $M_{persp \rightarrow ortho}$ 的第三行必为 $(0, 0, A, B)$,有
$$\begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} x\\y\\-n\\1 \end{bmatrix}=-n^2$$即有
$$-An + B = -n ^ 2$$
利用远平面 $z$ 不变
取点 $(0, 0, -f, 1) ^ T$,即有
于是
$$\begin{bmatrix} 0 & 0 & A & B \end{bmatrix}\begin{bmatrix} 0\\0\\-f\\1 \end{bmatrix}=-f^2$$即有
$$-Af + B = -f ^ 2$$
于是
$$\begin{cases} -An + B = -n ^ 2\\ -Af + B = -f ^ 2 \end{cases}$$所以
$$A = n + f, B = nf$$
$$M_{persp \rightarrow ortho}=\begin{bmatrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n + f & nf\\ 0 & 0 & -1 & 0 \end{bmatrix}$$最后
$$M_{persp} = M_{ortho}M_{persp \rightarrow ortho} = \begin{bmatrix} \frac{2n}{r - l} & 0 & \frac{r + l}{r - l} & 0\\ 0 & \frac{2n}{t - b} & \frac{t + b}{t - b} & 0\\ 0 & 0 & -\frac{f + n}{f - n} & -\frac{2nf}{f - n}\\ 0 & 0 & -1 & 0 \end{bmatrix}$$透视投影中视锥的定义 (假设 $l = -r, b = -t$)
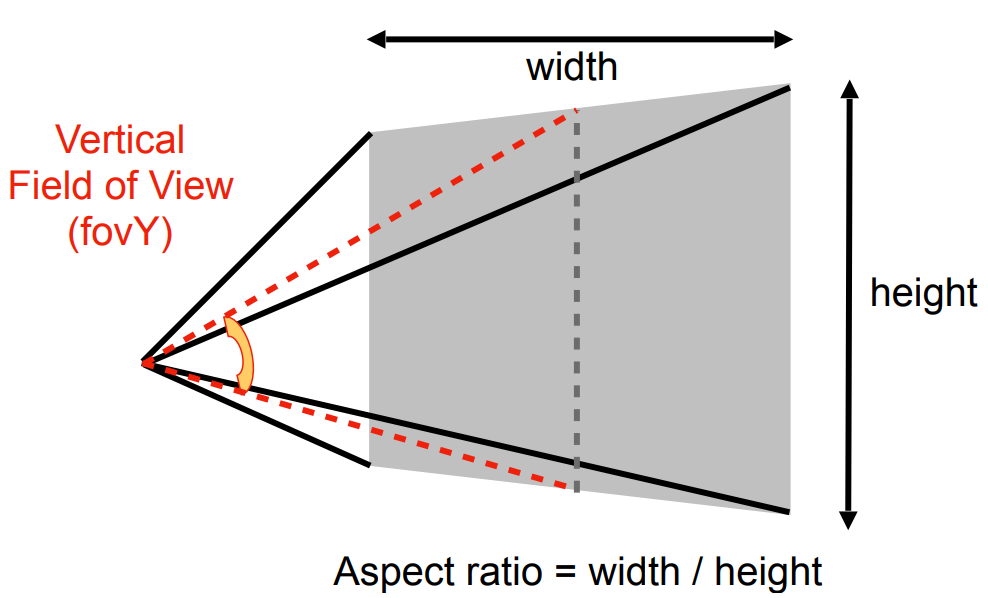
- aspect ratio 宽高比
- field-of-view fov 垂直可视角度
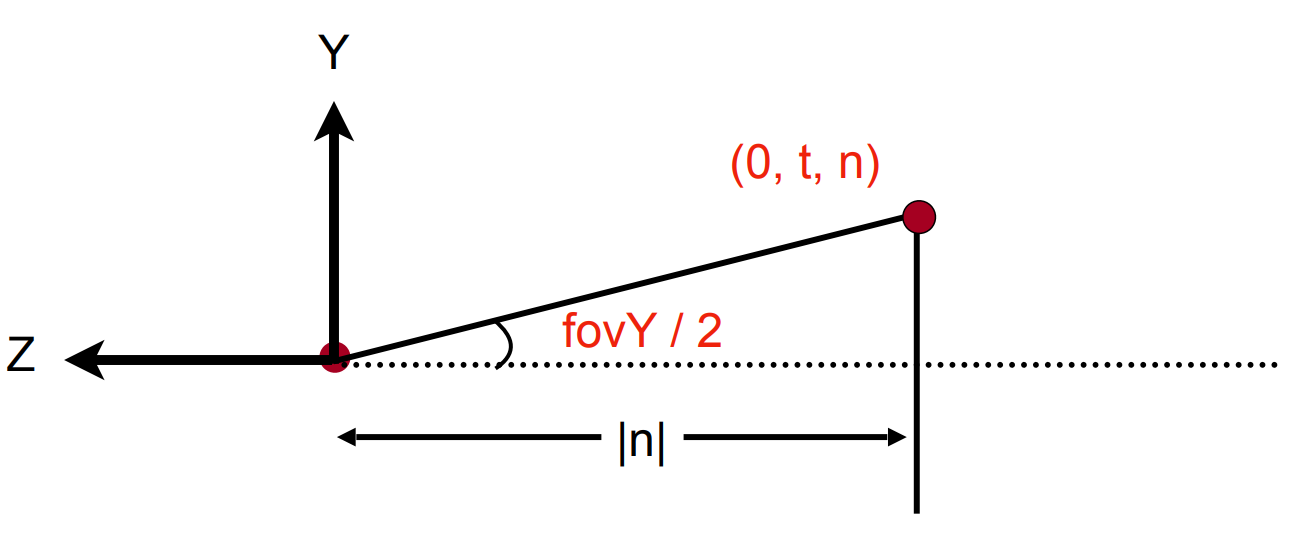
故用 fov 和 aspect ratio 替换可以得到
$$M_{persp} = \begin{bmatrix} \frac{1}{\tan(\text{fov} / 2)\cdot \text{aspect}} & 0 & 0 & 0\\ 0 & \frac{1}{\tan(\text{fov} / 2)} & 0 & 0 \\ 0 & 0 & - \frac{f + n}{f - n} & -\frac{2fn}{f - n}\\ 0 & 0 & -1 & 0 \end{bmatrix}$$对比 glm 代码是一致的
1 | template<typename T> |
法线变换矩阵 (The Normal Transformation Matrix)
在实现光照时,我们需要将法线变换到观察空间/世界空间,但是在不均匀缩放等情况下,直接对法线变换是错误的,这里就需要法线变换矩阵了。
设 $\boldsymbol{T}$ 为切向量,$\boldsymbol{N}$ 为法向量。设切向量的变换矩阵为 $M$,变换后的切向量为 $\boldsymbol{T’} = M\boldsymbol{T}$,设正确的法线变换矩阵为 $G$,使得 $\boldsymbol{N’} = G\boldsymbol{N}$,变换后的法线与切线仍然是垂直的,于是有
$$\boldsymbol{N’} \cdot \boldsymbol{T’} = (G \boldsymbol{N}) \cdot (M \boldsymbol{T}) = (G\boldsymbol{N})^T(M \boldsymbol{T}) = \boldsymbol N ^ T G^T M \boldsymbol T = \boldsymbol N \cdot \boldsymbol T = 0$$
故有
$$G^TM = I \Rightarrow G = (M^{-1})^T$$


