定义 字符串 字符串 $s$ 连续的一段字符组成的串叫做字符串,更广义地,任何一个由可比较大小的元素组成的数组都可称为字符串。字符串的下标从 $0$ 开始,长度为 $length(s)$。
后缀 后缀:$suffix(i)$ 表示字符串 $s$ 从第 $i$ 个位置开始的后缀,即由 $s[i]$ ~ $s[n - 1]$ 组成的子串。
比较 两个字符串大小的比较,从首位开始,一位一位地按照 $ASCII$ 码比较,如果从某位置开始不相同,则认为该位置处字符 $ASCII$ 码小的字符串小;注意 ,同一个字符串的两个后缀是不可能相等的,因为无法满足相等的必要条件长度相同 。
后缀数组 后缀数组:$sa[]$ 是一个一维数组,保存了对字符串 $s$ 的所有后缀排序后的结果。 表示第 $i$ 小的后缀在原串中的起始位置。
名次数组:$rank[]$ 是一个一维数组,按起始位置保存了每个后缀在 $sa[]$ 中的排名,$rank[i]$ 表示 $suffix(i)$ 的排名,即 $rank[sa[i]] = i$ (第 $i$ 小的后缀排名为 $i$)
高度数组:$height[]$ 是一个一维数组,保存了相邻两个后缀的最长公共前缀(Longest Common Prefix,LCP)长度。
$$height[i]=\left \{\begin {matrix}
0 & i = 0 & \\
LCP(suffix(sa[i]), suffix(sa[i - 1])) & i > 0 &
\end {matrix} \right.$$
即 $height[i]$ 表示存在的最大的 $x$,满足对于任何 $k \in [0, x)$ 有 $s[sa[i] + k] = s[sa[i - 1] + k]$
构造 朴素算法 如果我们直观地通过定义来构造后缀数组与名次数组(即将每个后缀看做独立的字符串进行快速排序),时间复杂度为 $O(n ^ 2 \log n)$,但平方级别的复杂度通常是无法承受的。
上述构造方法的瓶颈在于字符串的比较,原串的每个后缀的长度是 $O(n)$ 级别的,最坏情况下需要 $O(n)$ 次比较操作才能得到两个后缀的大小关系。
基于 Hash 的优化 考虑对字符串进行 $Hash$。使用 $BKDRHash$ 算法 $O(n)$ 地预处理整个字符串后,可以 $O(1)$ 地得到任意子串的 $Hash$ 值,比较两个子串是否相等。
这样,我们就得到了一个改进算法:比较两个后缀时,二分它们的 $LCP$ 长度,并比较第一位不同的字符,总时间复杂度为 $O(n \log n \log n)$。
使用 $Hash$ 来构造后缀数组的好处在于时间复杂度较低,并且可以动态维护(使用 std::set),坏处在于 $Hash$ 的不稳定性。
倍增算法 上述两个算法,我们都是将两个后缀看做独立字符串进行比较,而忽视了后缀之间的内在联系。一个更优的算法是倍增算法,它的主要思路是,每次利用上一次的结果,倍增计算出从每个位置 $i$ 开始长度为 $2 ^ k$ 的子串的排名。
如果使用快速排序来实现双关键字排序,总时间复杂度为 $O(n \log n \log n)$,实现难度比 $Hash$ 的方法要低,并且更稳定。而考虑到每个关键字均为 $[-1, n)$ 的整数,我们可以使用 $O(n)$ 的基数排序,来将总时间复杂度将为 $O(n \log n)$。
但是这仍然在较大数据范围时比较吃力。
DC3算法 ①先将后缀分成两部分,然后对第一部分的后缀排序;
②利用①的结果,对第二部分的后缀排序;
③将①和②的结果合并,即完成对所有后缀排序;
时间复杂度为 $O(n)$,但常数极大,在较小数据范围时与倍增算法相比无明显优势,且实现复杂,性价比较低。
SA-IS算法 这是我推荐的方法,在下面重点介绍,其时间复杂度也为 $O(n)$,比 $DC3$ 算法效率高,常数较小且实现简单。
SA-IS算法 以下内容的参考来源详见文末。
记号 为方便描述,我们先规定一些记号。
以下记号与诱导排序相关
$C\text{-}$ 表示后面在字典序里更小的数据 ,$C\text{+}$ 则相反,$C\text{*}$ 则是 $C\text{+}$ 的变体,如果$C\text{+}$ 前是 $C\text{-}$,那么这个就是 $C\text{*}$。
诱导排序 如何利用 $C\text{*}$ 完整地找出对应的 $C\text{-}$,$C\text{+}$ ?由于 $C\text{+}$ 的机制与 $C\text{-}$ 的机制差不多,所以重点说说 $C\text{-}$ 就好了(更详细的请见文末论文链接)。$C\text{-}$ 的遍历过程是通过按照字典序遍历所有出现过的字母。在每次处理当前字母的时候顺序把已经在栈里的字母重新压栈,并且把接下来需要处理的字母进行压栈。如果当前字母前面有 $C\text{-}$,那么这些 $C\text{-}$ 都会顺序入栈。这样就能保证数据不重复。随着字母的不断往后迭代,就能保证所有字母都能迭代到,从而保证数据不漏。因为 $C\text{*}$ 是有序的,那么 $C\text{-}$,$C\text{+}$ 就是有序的。
以上就是诱导排序的基本算法。$C\text{*}$ 排序需要利用到另外一个算法(LSD radix sort)。它这个算法的核心在于,每次都利用单个字母位进行桶排序(bucket sort),这样就能保证 $C\text{*}$ 符合字典序。进而保证整个诱导排序都是正确的。
基本框架
分类所有后缀文本 $S$ (较小的) 和 $L$ (较大的)
扫描倒序字符串确定每一个后缀的类型
扫描t数组确定所有的LMS子串
对所有的LMS子串进行诱导排序
对每一个LMS子串重新命名,生成新的串
递归计算 $sa1$
利用 $sa1$ 进行诱导排序,计算 $sa$
回收内存
伪代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 sais(T,A) for i = n to 1 do if (T[i] >lex T[i+1 ]) typ[i] <- L if (typ[i+1 ] = S) typ[i+1 ] = S* else typ[i] <- S begin <- {} for j = 1 to n do if (typ[j] = S*) if (begin = {}) begin <- j else end <- p T'[q] <- CharacterFor(begin,end) q <- q + 1 begin <- end If (everyCharacterInT' IsUnique(T')) A <- countingSort(T' ) return A else A <- sais(T',A) for k = 1 to n do if (A[k] != {}) if (typ[A[k]-1] = L) A <- writeToLBucketForCharacter(T[A[k]-1]) for l = n to 1 do if (A[l] != {}) if (typ[A[l]-1] = S) A <- writeToSBucketForCharacter(T[A[l]-1]) return A
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 function SA -IS (S ): t = bool[] S1 = int[] P = int[] bucket = int[] 扫描倒序字符串确定每一个后缀的类型 -> t 扫描t数组确定所有的LMS子串 -> P 对所有的LMS子串进行诱导排序 对每一个LMS子串重新命名,生成新的串S1 if S1中的每一个字符都不一样: 直接计算SA1 else SA1 = SA-IS(S1) # 递归计算SA1 利用SA1来进行诱导排序,计算SA return SA
后缀类型 对于每一个后缀 $suffix(S,i)$,当 $suffix(S,i)$ < $suffix(S,i+1)$ 时,是 $S$ 型后缀。当 $suffix(S,i)$ > $suffix(S,i+1)$ 时,是 $L$ 型后缀。对于特殊的后缀$suffix(S,|S|)= $# (具体实现可以简化掉),它默认为 $S$ 型。
例如,对于字符串 $mmiissiissiippii$,每一后缀的类型为:
1 2 3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 S[i]: m m i i s s i i s s i i p p i i t[i]: L L S S L L S S L L S S L L L L S
既然我们需要得知每一个后缀类型,就需要一个快速的算法来计算。在此之前,我们发现它们有如下的性质:
引理 : (后缀类型递推性质) 对于任意的 $i \in [0,|S| - 1]$:
如果 $t[i]=S-typet[i]=S-type$,当且仅当下面任意一项成立:
$S[i]<S[i+1]$
$S[i]=S[i+1]$ 且 $t[i+1]=S-type$
如果 $t[i]=L-type$,当且仅当下面任意一项成立:
$S[i] > S[i+1]$
$S[i]=S[i+1]$ 且 $t[i+1]=L-type$
证明: 这里证明 $S$ 型的,$L$ 型是类似的。对于第一种情况,显然是成立的。对于第二种情况,我们设 $suffix(S,i)=aA,suffix(S,i+1)=aB$。由于第一个字符是相同的,因此我们需要比较 $A$ 和 $B$ 的大小。因为它们是连续的后缀,所以 $A=suffix(S,i+1),B=suffix(S,i+2)$。由于我们是从右往左推出 $t$,所以 $A$ 与 $B$ 的关系实际上可以由 $t[i+1]$ 给出。故$t[i]=t[i+1]$。
因此,我们可以在 $O(|S|)$ 的时间内,推出整个 $t$ 数组。
关于后缀类型,我们还可得出另外一个比较重要的性质:
引理: (后缀类型指导排序) 对于两个后缀 $A$ 和 $B$,如果 $A[0]=B[0]$ 且 $A$ 是 $L$ 型,$B$ 是 $S$ 型,则 $A < B$。
证明: 设 $A=abX,B=acY$,这里假设 $a \neq b,a \neq c$。因为 $A$ 是 $S$ 型,所以可知$a < b$。同理,$B$ 是 $L$ 型,可知 $a$ > $c$。故 $c < a < b$,所以 $A < B$。如果$a=b,a=c$,则我们可以将第一个字符去掉,得到新的后缀来进行比较。根据上面引理 ,去掉第一个字符后的后缀类型不变。因此我们可以通过这样的操作从而变为第一种情况。
LMS子串 然而光有后缀类型,还不足以进行排序。因此我们在后缀类型的 $S$ 型中挑出特别的一类,记为 $*$ 型。$*$ 型是 $S$ 型的一种,它的特殊之处在于它要求它的左边的后缀必须是 $L$ 型的。依然以 $mmiissiissiippii$ 为例:
1 2 3 4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 S[i]: m m i i s s i i s s i i p p i i t[i]: L L S S L L S S L L S S L L L L S * * * *
可以将其理解为一连串的 $S$ 型中最靠左的一个。$LMS (LeftMost S-type)$ 也正是这个意思。同时我们注意到,后缀 # 始终是 $\text{*}$ 型的。
对于每一个 $\text{*}$ 型所对应上的字符,我们称为 $LMS$ 字符。上面的示例中,下标为$2,6,10,16$ 都是 $LMS$ 字符。
通过观察,我们发现LMS子串具有以下的性质:
引理: # 是最短的 $LMS$ 子串。
引理: 对于任意的非 # 的 $LMS$ 子串,其长度大于 $2$。
证明: 因为两个 $LMS$ 字符中间必定有一个 $L$ 型的后缀。
引理: (原串折半) 一个字符串中 $LMS$ 子串的数量不超过 $\lceil |S|/2 \rceil$。
引理: 一个字符串的所有LMS子串的长度之和为$O(|S|)$)。
此外,对于 $LMS$ 子串间的大小比较,除了对每个字符的字典序进行比较外,还要对比每个字符所对应的后缀类型。$S$ 型的有更高的优先权,因为 $S$ 型的后缀字典序更大。只有当每一个字符与其后缀类型都相同时,这两个 $LMS$ 子串才被称为是相同的。
之所以这样定义,是因为在之后我们会利用 $LMS$ 子串来进行对后缀的排序。如果缺少后缀类型的信息,就不能够任务。
我们可以利用基数排序在 $O(|S|)$ 的时间内对所有的 $LMS$ 子串排序。对 $LMS$ 子串排序完后,我们按照字典序依次重新命名,注意,如果两个 $LMS$ 子串相同,则使用同样的名称。这样给每个 $LMS$ 子串命名后,按照其子串原有的顺序排出一个新串$S1$。继续以mmiissiissiippii为例:
1 2 3 4 5 6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 S[i]: m m i i s s i i s s i i p p i i t[i]: L L S S L L S S L L S S L L L L S * * * * new name 2 2 1 0 S1: 2 2 1 0
这样有什么用呢?我们发现,这实际上是将所有 $*$ 型的后缀进行了缩减,从而减小了问题的规模。对于这一点,我们有如下的引理:
引理: (问题缩减) $S1$ 中两个后缀的字典序关系,就是 $S$ 中对应的 $*$ 型后缀的字典序关系。
证明: 我们可以将 $S1$ 视为是将 $*$ 后缀中不重合的部分进行切割并缩减。这样每一个 $LMS$ 子串就可作为一个整体来进行比较。从而保持了这两者的一致性。
需要注意的是这里只是 $*$ 型后缀的字典序关系,与其它后缀无关。
从SA1诱导至SA 从上面的引理我们得知,只要获得了$S1$ 的后缀数组 $SA1$,就可以得到所有 $$ 型后缀的相对顺序。如果我们可以利用 $ $ 型后缀的相对顺序来对其它的 $L$ 型和 $S$ 型后缀进行排序,就可以完成后缀数组的计算。
在这里我们先假定 $SA1$ 已经计算出来,只需考虑如何计算 $SA$。在这之前,我们先观察一下后缀数组的形式。以 $aabaaaab$ 为例,它的后缀数组是这样的:
1 2 3 4 5 6 7 8 9 aaaab aaab aab aabaaaab ab abaaaab b baaaab
不难发现,首字母相同的后缀是连续排布的,这一点可以用反证法来证明。因此我们可以利用桶排序的思想,为每一个出现过的字符建立一个桶,用 $SA$ 数组来存储这些桶,每个桶之间按照字典序排列,这样就可以使后缀数组初步有序。
我们对每个后缀都赋予了一个后缀类型,那么在首字母一样的情况下,$S$ 型或 $L$ 型会连续分布吗?答案是肯定的。因为首字母相同的后缀如果后缀类型不同,则相对顺序是确定的。因此易知不会出现 $S$ 型和 $L$ 型交替出现的情况。更进一步,由于$L$ 型后缀更小,因此总是先排布 $L$ 型后缀,再排布 $S$ 型后缀。因此每一个字符的桶可以分为两部分,一个用于放置 $L$ 型后缀,另一个则用于 $S$ 型后缀。为了方便确定每一个桶的起始位置,$S$ 型后缀的桶的放置是倒序的。
但是如果首字母和后缀类型都一致,我们不能直接快速地判断大小关系。在这里就要利用到诱导排序了。
诱导排序的过程分为以下几步:
将 $SA$ 数组初始化为每个元素都为 $-1$ 的数组。
确定每个桶 $S$ 型桶的起始位置。将 $SA1$ 中的每一个 $*$ 型后缀按照 $SA1$ 中的顺序放入相应的桶内。
确定每个桶 $L$ 型桶的起始位置。在 $SA$ 数组中从左往右扫一遍。如果$SA[i]>0$ 0且 $t[SA[i]-1]=L-type$,则将 $SA[i]-1$ 所代表的后缀放入对应的桶中。
重新确定每个桶 $S$ 型桶的起始位置,因为所有的 $*$ 型后缀要重新被排序。由于$S$ 型桶是逆序排放的,所以这次从右至左地扫描一遍 $SA$ 。如果 $SA[i]>0$ 且$t[SA[i]-1]=S-type$,则将 $SA[i]-1$ 所代表的后缀放入对应的桶中。
这样我们就可以完成从 $SA1$ 诱导到 $SA$ 的排序工作。这里简单说明一下为什么这样做是正确的:首先对于所有的 $*$ 型后缀,都是有序排放的。从左至右扫描 $SA$ 数组实际上就是按照字典序扫描现有的已排序的后缀。对于两个相邻的 $L$ 型后缀 $A$ 和 $B$,这里假设 $|A|>|B|$,则必定有 $A>B$。由于 $B$ 会被先加入 $SA$ 中,所以我们保证了$A$ 和 $B$ 之间的有序性。又因为 $L$ 型桶是从左往右的顺序加入的,所以所有的 $L$ 型后缀会逐步地按顺序加入到 $SA$ 中。最后所有的 $L$ 型后缀将会有序。
对于 $S$ 型后缀,除了要注意是相反的顺序和需要重新对 $*$ 型后缀排序外,其余的原理与 $L$ 型的排序类似。
如果 $S1$ 中每一个字符都不一样,则可以直接利用桶排序直接计算 $SA1$。
否则,递归计算 $SA1$。就如之前的算法框架所展示的一样。
对 $LMS$ 子串排序 到这里,$SA-IS$ 算法几乎已经结束了,只是还有一个问题需要解决,就是对 $LMS$ 子串的排序。
这个算法依然是诱导排序。
与之前从 $SA1$ 诱导到 $SA$ 的算法一样,只是我们这里将第二步改为:
确定每个桶 $S$ 型桶的起始位置。将每一个 $LMS$ 子串的首字母按照任意顺序放入对应的桶中。
待算法完成,我们会获得一个 $SA$ 数组,其中 $LMS$ 子串之间是排好了序的。
算法正确性证明详见文末链接
时间复杂度 在之前的讨论中,我们已经成功的运用诱导排序使每一步都是 $O(|S|)$。但是由于有一个递归的过程,时间复杂度似乎并不一定是线性的。
我们注意到,每次递归都是计算 $S1$ 的后缀数组。如果我们能够知道 $S1$ 的规模,就能够计算 $SA-IS$ 的时间复杂度。
因为 $|S1| \leq |S|/2$。因此每一层的递归的问题规模都会减半。因此我们可以用以下的递归式来表示时间复杂度:
$T(n)=T(n/2)+O(n)$
求解可得:
$T(n)=O(n)$
因此总时间复杂度是 $O(n)$ 的。
对于这个递归式,我们可以理解为是递归了$O(logn)$ 层,其中每一层的问题规模从小到大排序是 $2^0,2^1,2^2,\cdots,2^{logn}$。因此总复杂度就是对它们进行求和:
$\sum_{k = 0}^{logn}2^k = 2 \times 2^{logn}=O(2^{logn}) = O(n)$
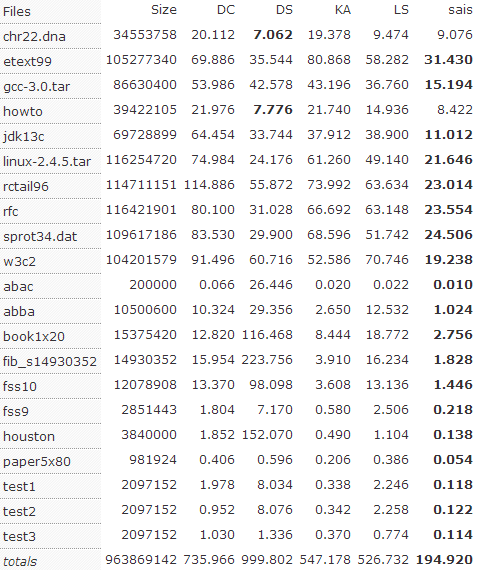
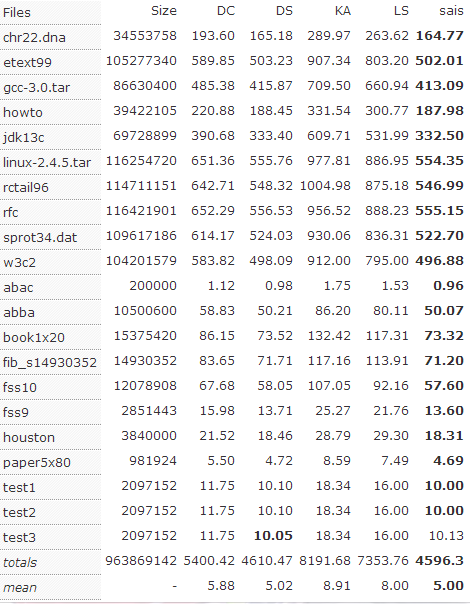
性能对比
从上面的结果可以看出,$SA-IS$ 算法速度上明显优于 $DC3$ 算法,并且数据规模越大,两者的速度差距越明显。
代码 论文代码链接
以下是经过我简化实现的 $C++$ 代码,重复利用了数组,且利用了 $rk$ 和 $ht$ 数组,从而进一步减小内存消耗。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 template <size_t size>struct SuffixArray { bool type[size << 1 ]; int bucket[size], bucket1[size]; int sa[size], rk[size], ht[size]; inline bool isLMS (const int i, const bool *type) return i > 0 && type[i] && !type[i - 1 ]; } template <class T > inline void inducedSort (T s , int *sa , const int len , const int sigma , const int bucketSize , bool *type , int *bucket , int *cntbuf , int *p ) { memset (bucket, 0 , sizeof (int ) * sigma); memset (sa, -1 , sizeof (int ) * len); for (register int i = 0 ; i < len; i++) bucket[s[i]]++; cntbuf[0 ] = bucket[0 ]; for (register int i = 1 ; i < sigma; i++) cntbuf[i] = cntbuf[i - 1 ] + bucket[i]; for (register int i = bucketSize - 1 ; i >= 0 ; i--) sa[--cntbuf[s[p[i]]]] = p[i]; for (register int i = 1 ; i < sigma; i++) cntbuf[i] = cntbuf[i - 1 ] + bucket[i - 1 ]; for (register int i = 0 ; i < len; i++) if (sa[i] > 0 && !type[sa[i] - 1 ]) sa[cntbuf[s[sa[i] - 1 ]]++] = sa[i] - 1 ; cntbuf[0 ] = bucket[0 ]; for (register int i = 1 ; i < sigma; i++) cntbuf[i] = cntbuf[i - 1 ] + bucket[i]; for (register int i = len - 1 ; i >= 0 ; i--) if (sa[i] > 0 && type[sa[i] - 1 ]) sa[--cntbuf[s[sa[i] - 1 ]]] = sa[i] - 1 ; } template <typename T> inline void sais (T s, int *sa, int len, bool *type, int *bucket, int *bucket1, int sigma) int i, j, bucketSize = 0 , cnt = 0 , p = -1 , x, *cntbuf = bucket + sigma; type[len - 1 ] = 1 ; for (i = len - 2 ; i >= 0 ; i--) type[i] = s[i] < s[i + 1 ] || (s[i] == s[i + 1 ] && type[i + 1 ]); for (i = 1 ; i < len; i++) if (type[i] && !type[i - 1 ]) bucket1[bucketSize++] = i; inducedSort(s, sa, len, sigma, bucketSize, type, bucket, cntbuf, bucket1); for (i = bucketSize = 0 ; i < len; i++) if (isLMS(sa[i], type)) sa[bucketSize++] = sa[i]; for (i = bucketSize; i < len; i++) sa[i] = -1 ; for (i = 0 ; i < bucketSize; i++) { x = sa[i]; for (j = 0 ; j < len; j++) { if (p == -1 || s[x + j] != s[p + j] || type[x + j] != type[p + j]) { cnt++, p = x; break ; } else if (j > 0 && (isLMS(x + j, type) || isLMS(p + j, type))) break ; } x = (~x & 1 ? x >> 1 : x - 1 >> 1 ), sa[bucketSize + x] = cnt - 1 ; } for (i = j = len - 1 ; i >= bucketSize; i--) if (sa[i] >= 0 ) sa[j--] = sa[i]; int *s1 = sa + len - bucketSize, *bucket2 = bucket1 + bucketSize; if (cnt < bucketSize) sais(s1, sa, bucketSize, type + len, bucket, bucket1 + bucketSize, cnt); else for (i = 0 ; i < bucketSize; i++) sa[s1[i]] = i; for (i = 0 ; i < bucketSize; i++) bucket2[i] = bucket1[sa[i]]; inducedSort(s, sa, len, sigma, bucketSize, type, bucket, cntbuf, bucket2); } inline void getHeight (const char *s, const int len, const int *sa) for (int i = 0 , k = 0 ; i < len; i++) { if (rk[i] == 0 ) k = 0 ; else { if (k > 0 ) k--; int j = sa[rk[i] - 1 ]; while (i + k < len && j + k < len && s[i + k] == s[j + k]) k++; } ht[rk[i]] = k; } } template <class T > inline void init (T s , const int len , const int sigma ) { sais(s, sa, len, type, bucket, bucket1, sigma); for (register int i = 1 ; i < len; i++) rk[sa[i]] = i; getHeight(s, len, sa); } };
模板题 THOJ08 此题可以用来做性能测试模板题。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 #include <bits/stdc++.h> inline char read () static const int IN_LEN = 1000000 ; static char buf[IN_LEN], *s, *t; if (s == t) { t = (s = buf) + fread(buf, 1 , IN_LEN, stdin ); if (s == t) return -1 ; } return *s++; } template <class T >inline void read (T &x ) { static char c; static bool iosig; for (c = read(), iosig = false ; !isdigit (c); c = read()) { if (c == '-' ) iosig = true ; if (c == -1 ) return ; } for (x = 0 ; isdigit (c); c = read()) x = (x + (x << 2 ) << 1 ) + (c ^ '0' ); if (iosig) x = -x; } const int OUT_LEN = 1000000 ;char obuf[OUT_LEN], *oh = obuf;inline void writeChar (char c) if (oh == obuf + OUT_LEN) fwrite(obuf, 1 , OUT_LEN, stdout ), oh = obuf; *oh++ = c; } template <class T >inline void print (T x ) { static int buf[30 ], cnt; if (x == 0 ) { writeChar(48 ); } else { if (x < 0 ) writeChar('-' ), x = -x; for (cnt = 0 ; x; x /= 10 ) buf[++cnt] = x % 10 + 48 ; while (cnt) writeChar(buf[cnt--]); } } template <class T >inline void println (T x ) { print(x), writeChar('\n' ); } inline void flush () fwrite(obuf, 1 , oh - obuf, stdout ); } template <size_t size>struct SuffixArray { bool t[size << 1 ]; int sa[size], ht[size], rk[size]; inline bool islms (const int i, const bool *t) return i > 0 && t[i] && !t[i - 1 ]; } template <class T > inline void sort (T s , int *sa , const int len , const int sigma , const int sz , bool *t , int *b , int *cb , int *p ) { memset (b, 0 , sizeof (int ) * sigma); memset (sa, -1 , sizeof (int ) * len); for (register int i = 0 ; i < len; i++) b[s[i]]++; cb[0 ] = b[0 ]; for (register int i = 1 ; i < sigma; i++) cb[i] = cb[i - 1 ] + b[i]; for (register int i = sz - 1 ; i >= 0 ; i--) sa[--cb[s[p[i]]]] = p[i]; for (register int i = 1 ; i < sigma; i++) cb[i] = cb[i - 1 ] + b[i - 1 ]; for (register int i = 0 ; i < len; i++) if (sa[i] > 0 && !t[sa[i] - 1 ]) sa[cb[s[sa[i] - 1 ]]++] = sa[i] - 1 ; cb[0 ] = b[0 ]; for (register int i = 1 ; i < sigma; i++) cb[i] = cb[i - 1 ] + b[i]; for (register int i = len - 1 ; i >= 0 ; i--) if (sa[i] > 0 && t[sa[i] - 1 ]) sa[--cb[s[sa[i] - 1 ]]] = sa[i] - 1 ; } template <class T > inline void sais (T s , int *sa , const int len , bool *t , int *b , int *b1 , const int sigma ) { register int i, j, x, p = -1 , cnt = 0 , sz = 0 , *cb = b + sigma; for (t[len - 1 ] = 1 , i = len - 2 ; i >= 0 ; i--) t[i] = s[i] < s[i + 1 ] || (s[i] == s[i + 1 ] && t[i + 1 ]); for (i = 1 ; i < len; i++) if (t[i] && !t[i - 1 ]) b1[sz++] = i; sort(s, sa, len, sigma, sz, t, b, cb, b1); for (i = sz = 0 ; i < len; i++) if (islms(sa[i], t)) sa[sz++] = sa[i]; for (i = sz; i < len; i++) sa[i] = -1 ; for (i = 0 ; i < sz; i++) { for (x = sa[i], j = 0 ; j < len; j++) { if (p == -1 || s[x + j] != s[p + j] || t[x + j] != t[p + j]) { cnt++, p = x; break ; } else if (j > 0 && (islms(x + j, t) || islms(p + j, t))) break ; } sa[sz + (x >>= 1 )] = cnt - 1 ; } for (i = j = len - 1 ; i >= sz; i--) if (sa[i] >= 0 ) sa[j--] = sa[i]; register int *s1 = sa + len - sz, *b2 = b1 + sz; if (cnt < sz) sais(s1, sa, sz, t + len, b, b1 + sz, cnt); else for (i = 0 ; i < sz; i++) sa[s1[i]] = i; for (i = 0 ; i < sz; i++) b2[i] = b1[sa[i]]; sort(s, sa, len, sigma, sz, t, b, cb, b2); } template <class T > inline void getHeight (T s , int n ) { for (register int i = 1 ; i <= n; i++) rk[sa[i]] = i; register int j = 0 , k = 0 ; for (register int i = 0 ; i < n; ht[rk[i++]] = k) for (k ? k-- : 0 , j = sa[rk[i] - 1 ]; s[i + k] == s[j + k]; k++); } template <class T > inline void init (T s , const int len , const int sigma ) { sais(s, sa, len, t, rk, ht, sigma), rk[0 ] = 0 ; } }; const int MAXN = 1e6 + 10 ;char s[MAXN];int len;SuffixArray<MAXN> sf; int main () len = fread(s, 1 , MAXN, stdin ); sf.init(s, len + 1 , 256 ); for (register int i = 1 ; i <= len; i++) print(sf.sa[i]), writeChar(' ' ); flush(); return 0 ; }
参考资料
wiki百科 [A walk through the SA-IS algorithm - Screwtape’s Notepad](/document/A walk through the SA-IS algorithm - Screwtape’s Notepad.html)
SA-IS-OPT induced-sorting yuta256